The last Report to the Nation published by ACFE, stated that on average, fraud accounts for nearly the 5% of companies revenues.
> > on average, fraud accounts for nearly the 5% of companies revenues > > [](http://ctt.ec/q3j4X)
Projecting this number for the whole world GDP, it results that the “fraud-country” produces something like a GDP 3 times greater than the Canadian GDP.
No surprise than if companies and scholars are increasingly looking for way to prevent fraud and spot it when it occurs.
Particularly flourishing is the interest in methods and mathematical models useful for fraud detection, i.e. fraud analytics models.
[caption id=“attachment_516” align=“aligncenter” width=“660”] ‘fraud analytics’ interest from 2009 to 2015, source: Google Trends[/caption]
‘fraud analytics’ interest from 2009 to 2015, source: Google Trends[/caption]
During my working experience I got interested in a particular family of those models: unsupervised models.
Autonomous models for fraud detection
As greatly stated by professors Hastie and Tibshirani , unsupervised models are models that try to figure out things autonomously.
In fraud analytics, unsupervised models are those that do not require any previous knowledge of fraud schemes affecting the population you are looking at.
The reason why I decided to focus my attention to this family of models is simple:
Unsupervised fraud analytics models can be a really powerful weaponfor companies facing frauds events.
> > Unsupervised fraud analytics models can be a really powerful weapon for companies facing frauds events > > > > [](http://ctt.ec/U1nb_) > >
More specifically, those kind of models can be** applied when no previous fraud analytics** activity was** done** into the company in the past and no knowledge of undergoing fraud schemes is possessed.
Doesn’t sound sweet and magic?
Unfortunately, fraud is quite multi-face phenomenon, and may assumes different connotations in different situations.
From the analytical point of view, this means that it is not possible to find a model respecting the golden rule “one size fits all” (not a great academic jargon, I know…).
Two families of models
More formally, we can assume two main type of fraud analytics models:
distribution based models;
density based models.
Those models look for different kind of frauds:
the first for fraud that results in the population not following a distribution that otherwise should be followed;
the second for fraud that results in values isolated from the rest of the population .
Quite nice, but what kind of fraud schemes are we talking about?
Not pretending to be exhaustive, we can give two examples:
the _skimming_ scheme, consisting in not recording payments from customer, is easily caught by distribution models, because it results in not respecting the “natural” distribution of proceeds;
frauds on Expense reimbursements are more likely to be detected by density based models, if they are in a small number.
That said, what if we join those complementary families of models into one singular algorithm able to intercept a wider range of fraud events?
There is some evidence from literature that this can lead to an** increased accuracy (see for instance Hwang 2003 and Wheeler 2000 **) , and that led me to develop Afraus.
Afraus: three models for one score
Afraus is developed leveraging the complementarity concept, and is built using three different fraud analytics models:
the Benford’s Law, an empirical law used as a distribution model;
the Control Chart, a distribution model;
the Local Outlier Factor, a density model.
The conjunct use of those three models resulted in an increased precision over a population of audited data, as showed in paragraph Does really it work? Looking at real data
But before going to the results, let us see more closely the model.
The Benford’s Law
This model tests the data against a theoretical distribution of first digits, highlighting those records that significantly deviates from that distribution. I have written about Benford’s Law in a previous quite popular post, therefore I am not going to repeat myself here.
It is enough to say that this test has proven to be effective for the most different kinds of anomalies, from frauds in accounting data to social network suspicious behaviour . Generally speaking, Benford’s law is really good at looking for manipulation on datasets as a whole.
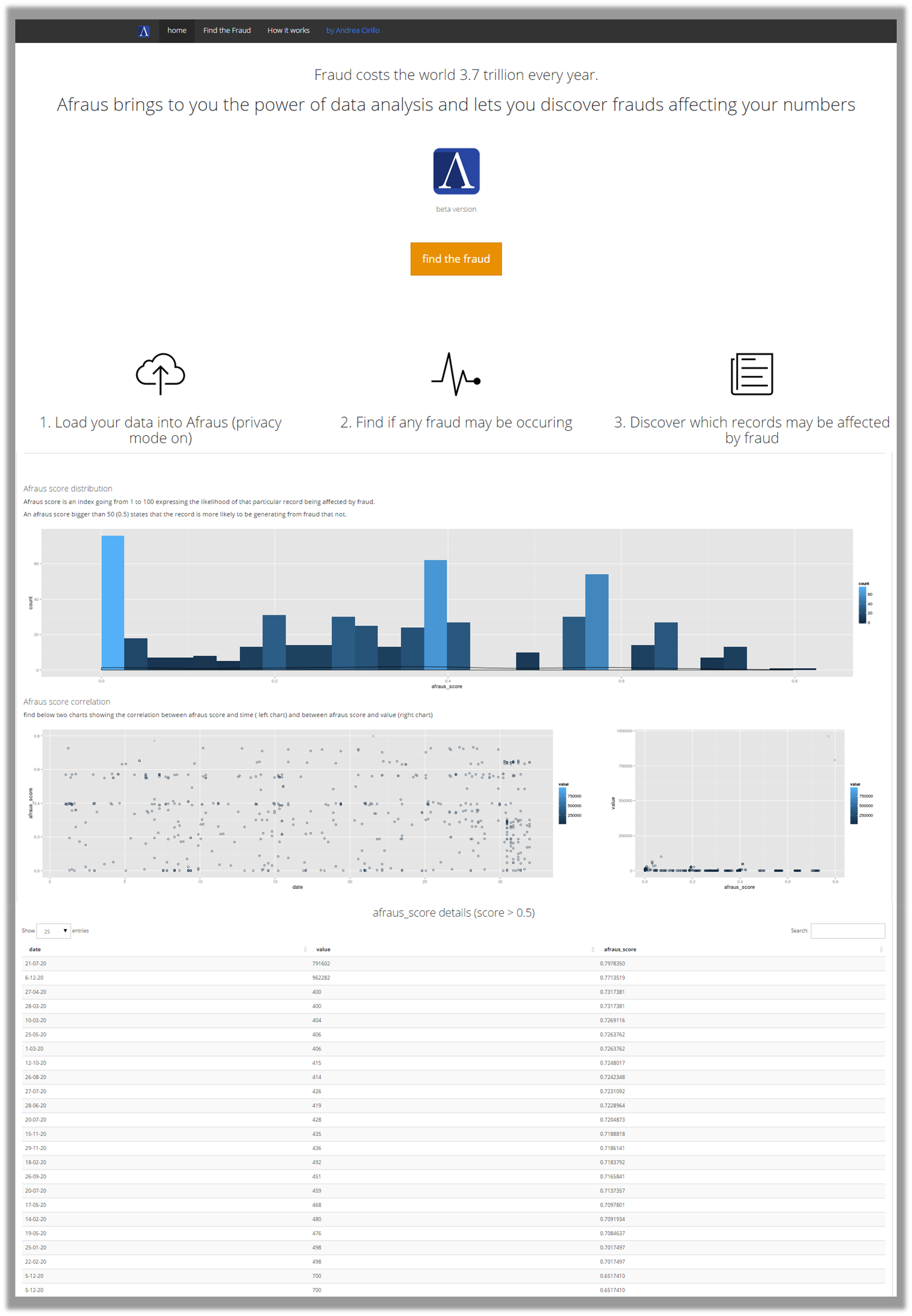
Afraus knows that, and uses it to understand how ‘clean’ is the population of data considered, assigning a score from 1 to 100 proportionate to the significant deviation from the expected frequency of the given digit. A 0 score is assigned to those records with no significant deviation.
Before moving on I have to mention some cautions that you need to use when applying Benford’s Law:
as stated by Durtschi, Hillison and Pacini not all kind of population are suitable to be tested using Benford’s Law, and even when they are, it is not obvious that they will comply with the Law, as clearly showed from professor Goodman .
Control Chart
Control charts are mainly known as a reliable tool for statistical process control.
Those kind of models derive from data a center line, an upper and a lower bound, highlighting as ‘out of control’ all records out of those limits.
As showed by Wheeler, even if those models assumes a normal distribution, they are also applicable to populations with non-normal distributions. This is mainly due to the robustness of the bounds derivation.
Afraus leverages the robustness of those charts to identify atypical data, calculating a score from 1 to 100 proportionate to the distance from the upper/lower bound, and assigning a 0 score to the records falling within the bounds.
Local Outlier Factor
Local Outlier Factor is a k-NN algorithm, based on the concept of density: the more isolated is a record, the higher is the likelihood it is originating from fraud. Afraus uses the LOF to intercept isolated values.
As for the two previous models,** Afraus assigns a score from 0 to 100** to each record within the population being analyzed.
Given the formulation of the Local Outlier Score a 0 score is given to records less or equal to 1 and a 1 to 100 score is given tho the other records, using the maximum level of LOF to set the 100 score.
The final score
As seen within the previous paragraphs, Afraus leverages the concept of complementarity, joining together different models.
For each model Afraus calculates a “compliance-score” ranging from 0 to 100. In order to express a synthetic judgment on each record, a final score is calculated.
This score is simply defined as the weighted average of the three “compliance-scores”.
How can I give it a try?
If you are interested in testing the algorithm I have developed a nice web application, based on Shiny, named Afraus:
try the Afraus web app
Using the Afraus web application you can test the algorithm with your own custom data, and give a look to the results into details.
Of course, I have already done some test on real data, and I am going to show you the results in the next paragraph.
Does it really work? Looking at real data
As always is the case for fraud analytics, having developed a nice algorithm is not enough, you need to show that it works and does its job properly.
Therefore In order to check the validity of the complementary concept, I have made the following test:
I have applied the three models separately on a population of labelled data with frauds, resulting from a fraud audit, and then I have applied Afraus on the same population.
After that I have determined the confusion matrix and the precision score , measuring how good performed Afraus against the single models it is made of.
Those were the results:
As you can see, Afraus brings a sensible improvement into the precision index, suggesting that a good way was taken.
Nevertheless as is often the case, it seems to be quite a long journey, and more developments are coming.
Could it work better? currently working on…
As shown in previous paragraph, Afraus has shown to be an interesting unsupervised fraud detection algorithm, able to detect real cases of fraud having no previous hint at all.
But, as said, I got interested into unsupervised models because they can make a good job for companies even when they have no previous knowledge about fraud and fraud detection.
That is why, after smiling for a while at the graph above, I asked myself: how can I make that 0.17 growth always avoiding to ask the analyst any specification?
This question led me to define the development path of Afraus: integrating more fraud detection models, dynamically chosen by the algorithm itself.
This implies some conditional instructions based on tests of the assumptions taken for true from the different models.
Let’s make an example: we could integrate regression models and choose the type of regression equation based on the R squared parameter.
Afraus is currently developed in R language, and I am committing changing to the code on a Github public repo, start watching it if you would like to keep an eye on the project.
Conclusion
Fraud is a dangerous animal, threatening companies and the economy as a whole. Fraud Analytics can be a great ally into the battle with this public enemy, that is why it is receiving increasing attention from companies and academy. Among fraud analytics models, unsupervised models can be really precious for the first fraud detection activities in a company, and a complementary approach can make them even more precious.
Knowing that, I have developed for professional purposes Afraus, an unsupervised fraud detection algorithm aimed at taking advantage of different models in order to easily scan population of data looking for fraud, without requiring any previous knowledge of undergoing fraud schemes or events affecting the data.
Have you ever tried this kind of approach? Which were your results?